Два стеклянных шара, и небоскрёб.

 

 Задача: Имеется два одинаковых стеклянных шарика и этажный дом. Необходимо предложить алгоритм, который

 за наименьшее количество бросаний определяет, с какого максимального этажа этот данный шарик не разобьётся.

 

Следует отметить, что предложенный алгоритм минимизирует кол-во испытаний в наихудшем случае. Т.е. тогда, когда нужный этаж находится в последний момент.

 

Решение:

Так как шариков всего два, то очевидно что, разбив первый, мы должны беречь второй и бросать его начиная  с проверенного этажа поднимаясь по одному этажу вверх.

 

Представим схему бросаний в виде дерева: Верхний его уровень обозначает первое бросание. Если шарик разбивается, то уходим на левую ветвь, если нет, то продолжаем увеличивать этаж, уходя на правую ветвь. В итоге глубина узла этого дерева соответствует номеру испытания, которое он обозначает, а степень «правости» узла соответствует высоте этажа данного испытания. Цифра в узле обозначает этаж, на котором проводилось испытание.

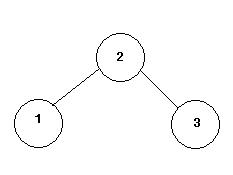
Данная схема обозначает, что сначала бросили со 2 этажа, если шар разбился бросили с 1 этажа, если не разбился, то с 3.

 

Бросив шар с какого-то этажа  мы либо разбиваем шарик, и идём начиная с первого вверх, либо не разбиваем шарик, и бросаем его тогда с какого-то другого этажа , причём

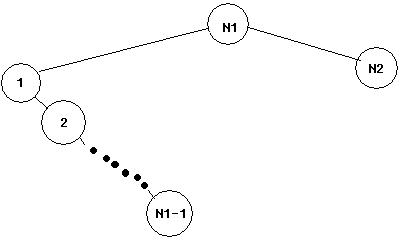
После испытания на  этаже мы будем действовать так же, как и после испытания на  этаже. (Потому что это единственно возможный вариант)

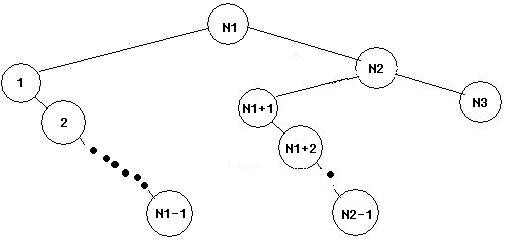
И так далее...

Т.к. длине алгоритма соответствует глубина дерева по соответствующим ветвям, то будем искать неизвестные ,, ...

такие, чтобы все ветви имели одинаковую, и при том минимальную длину, при заданном количестве узлов (равном кол-ву этажей ). Длинна алгоритма очевидно тогда будет равна номеру первого этажа .

Равенство ветвей    и    запишется следующим образом

,           (1)

а ветвей    и  

,            (2)

 продолжая получим

               (3)

               (4)

*****************

     (5)

выразив и подставив скобку из правой части (1) вместо скобки в левой части (2), получим

        (6)

выразим скобку из (6), и подставим в (3)

,

следуя этой логике получим:

.

В итоге

   (7)

Подставим в (7) выражение для  полученное из (7) заменой    .

,

продолжая эту логику получим

.

Мы выразили все  необходимые этажи через тот, на котором надо проводить первое испытание. Найдём и его.

 

Для этого нам необходимо найти такое минимальное , при котором  сможет достигнуть необходимого этажа.

Рассмотрим  как непрерывную функцию от

Найдём, когда она достигает максимума при фиксированном .

Т.к. нам нужны только целые числа, то максимальным будет  элемент.

Нам необходимо, что бы максимум , который равен  достигал максимального этажа

,

откуда

 

Задача решена. Найден алгоритм, и все необходимые данные об этажах в зависимости от высоты небоскрёба.

 

Для 100 этажного дома , округляя всегда в большую сторону, получим , а .